Il nostro Amico Antonio Bellomi è un tipo strambo: cordiale, ma cocciuto qualche volta! Per esempio, mi aveva mandato tempo fa questo articolo che in verità non parla affatto di fantascienza, ma racconta di alcuni misteri insiti nella matematica degli antichi. Ora, forse non tutti lo sanno, Antonio Bellomi è laureato in matematica.
Quando, ahinoi, gli ho detto che non potevo pubblicare un articolo che non trattava di fantascienza, ecco addirittura le minacce, “Se non pubblichi il mio trattato di matematica misteriosa, non ti lascio più pubblicare i mille e mille racconti che hai in magazzino con il mio nome!“
Capite bene che a questo punto ho dovuto cedere: perché davvero Antonio mi ha dato gratuitamente una quantità importante di suoi racconti! Quindi, abbiate pazienza, ma per due puntate (anche se non di seguito) vi parleremo di matematica antica e, sicuramente, divertente.
Questa è la prima puntata.
Grazie Antonio.
Chi ha inventato la matematica? si sono chieste legioni di studenti in preda alla più nera disperazione di fronte all’ennesima insufficienza in un compito scritto o in un’interrogazione di matematica. Probabilmente per loro la risposta è luciferina, perché solo un demone perverso poteva inventare quella che la maggior parte degli studenti di tutto il mondo considera una pura tortura mentale.
In realtà la matematica si è inventata da sola. O almeno le prime rudimentali basi della matematica sono state gettate in epoche così remote da perdersi nella notte dei tempi. Chi è stato il primo dei nostri antenati che ha avuto l’idea? Probabilmente più d’uno. Quando l’uomo ha cominciato a sviluppare le proprie facoltà cerebrali si sarà reso conto che della corrispondenza che poteva esistere tra una pecora e un suo dito. Tra due conigli e due dita. Tra dieci pesci e le dita delle due mani. Tra venti nemici avvistati su un’altura e le dita delle mani e dei piedi.
E le dita delle mani e dei piedi saranno serviti come prima notazione matematica, ancorché non durevolmente scritta, trasmissibile ad altri per facilitare la comunicazione. Da questa notazione fugace a una più duratura non dovrebbe essere passato molto tempo. La corrispondenza tra una pecora e un intaglio su un legno o su un osso non sarà certo sfuggita per molto tempo, una volta stabilita la relazione precedente. E infatti se si vanno a vedere tutte le primitive notazioni numeriche scritte si vede come quasi sempre i primi numeri sono stati scritti sotto forma di trattini o pallini: I, II, III, °, °°, °°°.
È evidente che il sistema rudimentale dei primi uomini a un certo punto non è più stato sufficiente per designare quantità più grandi e allora ecco che le menti più alacri hanno escogitato sistemi diverse di notazione e in un secondo tempo di calcolo.
A quando allora risale la prima notazione numerica che vada oltre la semplice ventina esprimibile con le dita di mani e piedi?
Nessuno è in grado di dirlo. I numeri esistono da millenni e ne abbiamo ritrovato le notazioni in ogni luogo della terra. Tuttavia c’è un elemento che non cessa di stupire gli studiosi. Com’è possibile che con concetti matematici abbastanza semplici gli antichi popoli siano riusciti a costruire edifici di grande complessità ingegneristica o a mettere a punto calendari raffinatissimi ed effettuare calcoli astronomici per i quali oggi si usano i computer?
Perché esiste questo scompensa tra teoria e pratica? Ma la teoria che è venuta alla luce, è veramente tutta la teoria conosciuta all’epoca, o a un livello superiore di iniziazione sacerdotale si tramandavano conoscenze segrete attinte da qualche altra civiltà? Conoscenze che andavano ben oltre quelle più semplici necessarie per compilare elenchi commerciali o cronistorie che tenevano conto dei nemici uccisi e catturati.
Le prime notazioni matematiche complete di cui abbiamo notizia certa risalgono a circa settemila anni fa e si sono sviluppate nell’area babilonese ed egizia. Ancora una vola l’Egitto torna quindi alla ribalta con quella che è forse la più grande conquista dell’umanità, la matematica.
Ma prima di parlare dell’Egitto, vediamo un momento quali sono le notazioni matematiche di alcune antiche civiltà, perché è interessante vedere quanti sono i punti in comune, come se tutto fosse derivato a un’unica matrice.
LA CIVILTÀ MAYA
La civiltà Maya ha avuto una durata tutto sommato abbastanza breve, dal 1.000 a.C. fino al XV secolo quando fu distrutta dall’invasione spagnola. Il suo periodo di massimo fulgore tra il 250 e il 900 d. C., quando si costruirono templi grandiosi, le cui iscrizioni su pietra si sono tramandate fino ad oggi, contrariamente ai testi manoscritti che furono quasi tutti distrutti dalla furia iconoclasta dei religiosi spagnoli. Di questi manoscritti, o codici, ne sopravvivono oggi solo quattro: il Codice di Dresda conservato nella Sächsische Landesbibliothek Dresden; ll Codice di Madrid conservato nel Museo Americano di Madrid; il codice di Parigi conservato alla Bibliothèque nationale in Paris e infine l’ultimo codice, scoperto solo di recente, il Codice Grolier, che fa parte di una collezione privata. Il Codice di Dresda è un trattato di astronomia e anche il Codice Grolier è un testo astronomico riguardante il ciclo di Venere. Per questo hanno una notevole importanza per spiegare la struttura della matematica Maya.
La scrittura dei codici è stata decifrata solo di recente, anche perché dotata di una struttura complessa fatta di glifi fonetici, contrariamente alla prima forma di scrittura epigrafica che era soprattutto ideografica, scomparsa per essere sostituita dai glifi fonetici.
Nella civiltà Maya rivestivano una grande importanza i sacerdoti che in pratica sovrintendevano allo svolgimento di tutte le attività sociali. Queste erano a loro volte legate al calendario, alla mitologia e all’astronomia, e di conseguenza i sacerdoti erano anche i depositari delle scienze matematiche.
La matematica Maya era molto avanzata a quel tempo, molto di più che in tante altre civiltà.
Il sistema numerico Maya era in base venti, o vigesimale. Chiaramente ha origine dall’abitudine di contare le dita delle mani e dei piedi. Ma rispetto a forme matematiche di altre civiltà presenta due interessanti innovazioni, l’invenzione dello zero e il sistema posizionale. Entrambi però utilizzati, a volte, in modo diverso da noi.
Vediamo però, prima, una tabella riportante i numeri coi glifi Maya, scritti sia nella forma orizzontale che in quella verticale. Nella tabella riportiamo prima la forma orizzontale, poi quella verticale.
Il sistema è chiaro è non ha bisogno di molte spiegazioni. È interessante notare come vengano utilizzati solo tre simboli in varie combinazioni: il punto, che vale un’unità, la sbarretta che vale 5 unità e lo zero, rappresentato da una conchiglia. Questo sistema a tre simboli ha il grosso vantaggio di ridurre il numero dei simboli necessari in un sistema vigesimale, se si dovessero applicare i criteri che sovrintendono al nostro sistema decimale. Infatti un sistema vigesimale costruito coi nostri criteri avrebbe ben 19 simboli: 1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,G,H,J,K.
Il sistema è posizionale. Si prenda per esempio il numero 25. La sbarretta che vale cinque unità è in basso, il puntino in di sopra in realtà non è uno, ma rappresenta la ventina e assume questo valore proprio in virtù della posizione sovrastante che assume.
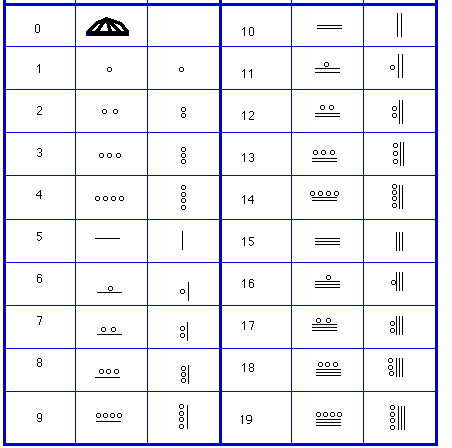
Ed ecco il numero 9449, così scomposto
1 x 9 = 9
20 x 12 = 240
20 x 20 x 3 = 1200
20 x 20 x 20 x 1 = 8000
Come direbbe un moderno cultore dell’algebra Booleana, il valore di un numero in base 20 si calcola moltiplicando il valore in ordine più basso per 200 (che vale 1), quello in seconda posizione per 201 , quello in terza posizione per 202 e così via.
Nel nostro esempio sarebbe (203 x 1) + (202 x 3) + (201 x 12) + (200 x 9).
La sua rappresentazione in glifi Maya qui sotto è riportata in colonna verticale, un numero per riga, tante righe quanti sono gli ordini di unità. Si legge in ordine decrescente: vale a dire che la riga in alto rappresenta l’ordine più alto e il pallino non è quindi un 1 ma un 1 moltiplicato per 203.
Nel computo però del calendario le cose vanno in maniera un po’ diversa. Per potere fare tornare più facilmente i conti dei giorni che compongono l’anno solare, gli astronomi introdussero una variante, nella terza posizione, di modo che il sistema non è più un sistema vigesimale puro. Infatti si comincia con le unità che sono 19 (18, perché si comincia da zero) e poi si prosegue con le ventine che vanno fino a 18 anche queste, ma nella terza posizione invece delle quattrocentine abbiamo le trecentossessantine (360), per poi tornare ai multipli di 20 nella quarta posizione.
Facciamo un esempio pratico.
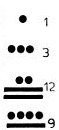
Prendiamo il numero 13.495
Nella struttura Maya verrà così scomposto
15 unità
8 – 8 x 20
17 – 17 x 18 x 20
1 – 1 x 18 x 20 x 20
Si noti, come già detto prima, la terza posizione, dove il fattore di moltiplica è 360 e non 400 come dovrebbe essere in un sistema vigesimale puro.
In glifi maya il numero va letto dall’alto in basso, in ordine decrescente ed è così rappresentato:
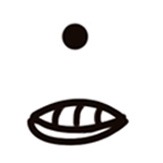
L’altra grande intuizione Maya è stata quello dello zero, rappresentato da una conchiglia
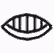
o da un fiore a quattro petali tagliato a metà, nelle due forme, orizzontale e verticale:
![]()
![]()
che ha un vero e proprio valore posizionale. Vediamo di chiarire il concetto.
Lo zero aveva valore posizionale, perché serviva a indicare nell’espressione di un numero che le unità di un certo ordine mancavano. Nella prima tabella, il numero venti non è raffigurato, ma per farlo si userebbe un pallino con sottostante la conchiglia. Il pallino è dunque in posizione “due” e indica il numero delle ventine, la conchiglia indica che la posizione delle unità semplici è zero. Se non ci fosse stata la conchiglia, il solo pallino avrebbe indicato il numero 1.
Stranamente i Maya, pur capaci di fare calcoli complessi non conoscevano probabilmente la moltiplicazione e sicuramente non la divisione. Ignoravano le frazioni. Eppure nonostante queste deficienze che secondo il nostro modo di pensare sembrerebbero precludere ogni forma di calcolo appena un po’ raffinato i Maya sono stati abilissimi architetti, costruendo piramidi che ancora oggi sopravvivono sfuggendo all’opera di una vegetazione oltremodo distruttiva e soprattutto mettendo a punto un calendario molto preciso.
Tutto questo sembra rappresentare un mistero, un mistero che si ripete anche presso altre civiltà. Come se in realtà esistessero conoscenze ancora più approfondite, ma appannaggio di una stretta cerchia di persone, la casta sacerdotale, che queste conoscenze non era disposta a dividere col volgo.
I numeri maya da 1 a 19, però, possono essere anche rappresentati in una forma cefalomorfa chiamata “variante a ritratto”, raffigurante una testa stilizzata, che rappresenta forse una divinità.

Veniva anche usato un simbolo cefalomorfo che rappresentava la luna e indicava il numero 20. Tale simbolo è abbinato al numero espresso secondo il normale sistema dei numeri.

ha svolto la sua attività nel campo dell’editoria per più di cinquant’anni. Ha diretto numerose testate dedicate al giallo, alla fantascienza, all’horror, al western e al fumetto. Ha scritto praticamente per ogni genere di letteratura popolare, dal giallo alla fantascienza, dal western alla narrativa per ragazzi e ha pubblicato più di trecento racconti su una miriade di periodici.



 Appassionato di fantascienza credo da sempre, ma scoperto di esserlo in quarta elementare quando mi hanno portato a vedere "
Appassionato di fantascienza credo da sempre, ma scoperto di esserlo in quarta elementare quando mi hanno portato a vedere "